Union

Union is a structured type that can contain different types of objects. Its definition looks similar to the definition of structure, but the difference is that only one of the fields can be stored at a time. Union reserves space only for a single object, and the compiler determines the amount of space needed based on the largest member in the union. Here is an example of an union definition, for an imaginary one-dimensional spreadsheet. Each cell of the spreadsheet can contain either a floating point number, a short string label, or a formula. For the formula, a separate structure is defined: union members can also be structures.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

#include <stdio.h>
#include <string.h>

// This structure stores an imaginary formula and two parameters
// (here we assume that the operation and two parameters are defined
// as small strings)
struct formula {
    char operation[10];
    char param1[10];
    char param2[10];
};

union u_types {
    float num;  // single number value in spreadsheet cell
    char label[20];  // text label in spreadsheet cell
    struct formula form;  // formula in spreadsheet cell
};

Below is a short, artificial example on how to use the union members. Our single-dimensional spreadsheet has 10 cells. This is done by using normal array based on the above specified union type. Each cell (array element) can have value that is either a floating point number, string label, or a formula. The below code directly continues from the above. It is worth paying attention on the referral to union members, e.g., on line 12: union members are accessed exactly like structure members, and when the member is itself a structure, there are multiple levels of structured members (separated with .).

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

int main(void)
{
    union u_types sheet[10];
    struct formula avg = { "AVG", "A2", "A3" };

    // Because t_label is an array, we need to use strcpy
    strcpy(sheet[0].label, "Header");

    // Direct assignment works because this is struct
    sheet[1].form = avg;

    printf("stored formula: %s(%s, %s)\n", sheet[1].form.operation,
           sheet[1].form.param1, sheet[1].form.param2);

    // This will "overwrite" the formula (partly)
    sheet[1].num = 5;
}

It is not generally possible to know which of the alternative types is currently stored in an union variable (apart from trivial examples as above). Therefore some additional method or variable is needed to track which type the union actually holds. Enumeration constants are a good fit for this.

Enumeration constants

Enumeration constants can be used to define variables that have one of the specified constants as a possible value. Here is an example of enumeration definition and its use:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

enum en_color {
    RED,
    GREEN,
    BLUE
};

void printColor(enum en_color col)
{
    switch(col) {
    case RED:
        printf("red\n");
        break;
    case GREEN:
        printf("green\n");
        break;
    case BLUE:
        printf("blue\n");
        break;
    } 
}

Compiler translates enumeration constants to constant integers, and they can be used in all normal expressions or functions similarly as if a constant integer was used in their place. By default the enumeration constants are assigned increasing values starting from zero: 'RED' equals to 0, 'GREEN' is 1, and 'BLUE' is 2 in the above example, but typically the integer values should not be directly used. The integer values for enumerations can also be given explicitly, as shown below:

1
2
3
4
5
6

/* Type Duration, some durations in seconds */
typedef enum {
    MINUTE = 60,
    HOUR = 60 * MINUTE,
    DAY = 24 * HOUR
} Duration;

Using enumeration constants, we can extend the above union example with the following definitions, to keep track of actual type stored in union variables:

1
2
3
4
5
6

enum en_types {
    UNSPEC,  // union content is unspecified
    NUMBER,  // union stores a number
    LABEL,   // union stores a string number
    FORMULA  // union stores a formula
};

The above specifies an enumeration constant en_types with four possible values: one for each of the union types specified above, and one value to indicate that the value is unspecified.

Below is a modified example, where each array element is cell structure instead of plain union. The structure has member type to keep track the type of the value stored in the union, and member value that is the previously defined union. With the structure we can keep track of the actual data type stored in the union.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66

// This structure stores an imaginary formula an two parameters
struct formula {
    char operation[10];
    char param1[10];
    char param2[10];
};

union u_types {
    float num;
    char label[20];
    struct formula form;
};

enum en_types {
    UNSPEC,  // union content is unspecified
    NUMBER,  // union stores a number
    LABEL,   // union stores a string number
    FORMULA  // union stores a formula
};

// one cell in spreadsheet: stores the type of the cell (enum)
// and the actual content (union, corresponding type indicated by enum)
struct cell {
    enum en_types type;
    union u_types value;
};

int main()
{
    struct cell sheet[10];
    struct formula avg = { "AVG", "A2", "A3" };

    int i;
    for (i = 0; i < 10; i++) {
        // initialization: all fields unspecified
        sheet[i].type = UNSPEC;
    }

    // Because label is an array, we need to use strcpy
    sheet[0].type = LABEL;
    strcpy(sheet[0].value.label, "Header");

    // Direct assignment works because this is struct
    sheet[1].type = FORMULA;
    sheet[1].value.form = avg;

    for (i = 0; i < 10; i++) {
        switch(sheet[i].type) {
        case LABEL:
            printf("%s\n", sheet[i].value.label);
            break;
        case NUMBER:
            printf("%f\n", sheet[i].value.num);
            break;
        case FORMULA:
            printf("%s(%s, %s)\n",
                   sheet[1].value.form.operation,
                   sheet[1].value.form.param1,
                   sheet[1].value.form.param2);
            break;
        case UNSPEC:
            printf("--\n");
            break;
        }
    }
}

Because of the new array structure, setting and accessing the values in the sheet array requires an additional indirection, as can be seen above (for example on lines 40 and 41): each array object is a cell structure, and each value field in cell structure is union, that requires additional field that indicates one of the types in union. Additionally, when setting the cell value based on one of the three possible data types, the type field of the structure needs to be updated, to keep track the actual type stored in the cell.

The above example also shows that because enumerations are constant integers, they can be used as part of a switch statement. Using the switch statement we can conveniently output the content of each cell using correct output format specifiers.

Static arrays

C supports also multidimensional arrays. In general, any number of array dimensions is possible, but here we focus just on two-dimensional arrays for clarity. Below is an example of a simple 3x3 static array and how it can be used.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

#include <stdio.h>

int main(void) {
    int matrix[3][3] = {{1,2,3}, {4,5,6}, {7,8,9}};
    int i,j;

    // Print the matrix in rectangular format
    for (j = 0; j < 3; j++) {
        for (i = 0; i < 3; i++) {
            printf("%d ", matrix[j][i]);
        }
        printf("\n");
    }
}

Line 4 in the main function defines variable matrix that is a two-dimensional 3x3 array. It is also initialized at the same time: note the initialization list notation of nested arrays for each row of the table. The format of the initialization list also illustrates what multidimensional arrays really are in C: arrays made of arrays.

After the initialization, the array is just printed on the screen as two-dimensional rectangle. The array is indexed similarly to one-dimensional array, but now there are two indexes in square brackets.

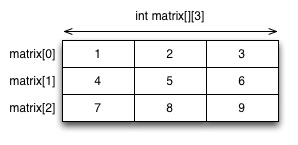
The diagram below illustrates how C implements a static two-dimensional array as the above. There are three arrays of integer arrays that have three integers each. In this case, all 9 elements are located in adjacent locations in memory.

Passing a static array as a function parameter has a special notation, as shown below. With a static two-dimensional array, the function parameter declaration must include the number of columns, so that the function can interpret the array data type correctly. The number of "first-dimension" members can be omitted: as with one-dimensional arrays, int arr[] is equal to int *arr, i.e., it can be handled as a pointer. The below example modifies the above by moving the array printing part into a dedicated function.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

#include <stdio.h>

void printArray(int arr[][3]) {
    int i,j;
    // Print the matrix in rectangular format
    for (j = 0; j < 3; j++) {
        for (i = 0; i < 3; i++) {
            printf("%d ", arr[j][i]);
        }
        printf("\n");
    }
}

int main(void) {
    int matrix[3][3] = {{1,2,3}, {4,5,6}, {7,8,9}};

    printArray(matrix);
}

A two-dimensional array can also be declared as an array of pointers (arr_p in below example), as shown below. This allows more flexible function interface, that will work with different sizes of arrays. Each pointer in the array points to the first member of a one-dimensional array.

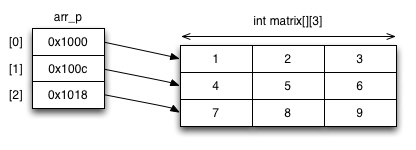
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

#include <stdio.h>

void printArray(int **arr, int xs, int ys) {
    int i,j;
    // Print the matrix in rectangular format
    for (j = 0; j < ys; j++) {
        for (i = 0; i < xs; i++) {
            printf("%d ", arr[j][i]);
        }
        printf("\n");
    }
}

int main(void) {
    int matrix[3][3] = {{1,2,3}, {4,5,6}, {7,8,9}};
    int *arr_p[3];

    for (int i = 0; i < 3; i++) {
        arr_p[i] = matrix[i];
    }

    printArray(arr_p, 3, 3);
}

The elements in 'arr_p' are of different data type than the first-degree elements of the "matrix" array: sizeof(arr_p[0]) returns the length of one int * pointer (8 bytes for 64-bit address), but sizeof(matrix[0]) is the length of an array consisting 3 integers (12 bytes in most systems). Therefore, the printArray() function above cannot be directly called using the matrix parameter. Fortunately C allows implicit translation of a one-dimensional integer array (matrix[i]) into a integer pointer to the first member of array (arr_p[i]), as done on line 19 above). After this operation calling printArray() function is possible.

Because now arr is delivered as pointer of pointers, it accepts different dimensions of arrays. Therefore we added two new parameters to function interface, to indicate the actual dimensions of the array. Otherwise the function implementation might not know the dimensions.

Dynamic allocated multi-dimensional arrays

Similarly to one-dimensional arrays, dynamic multi-dimensional arrays are allocated dynamically from heap using (possibly multiple) malloc() calls (in comparison to single malloc() call). A multidimensional array could be allocated in different ways, but here we focus on a straight-forward design: first, the high-level array is allocated, for storing a number of columns (i.e., one-dimensional arrays). Then, each column of the array is allocated with a separate malloc() call. The latter malloc() calls are similar to allocating a one-dimensional array. The first array holds a series of pointers to the beginning of one-dimensional arrays, and the second-degree arrays store the actual members. Here is an example:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

#include <stdio.h>
#include <stdlib.h>

void printArray(int **arr, int xs, int ys) {
    int i,j;
    // Print the matrix in rectangular format
    for (j = 0; j < ys; j++) {
        for (i = 0; i < xs; i++) {
            printf("%2d ", arr[j][i]);
        }
        printf("\n");
    }
}

int main(void) {
    int **arr_p;
    int xdim = 4;
    int ydim = 5;

    // first allocate array that points to arrays of rows
    // (notice the data type in sizeof operation)
    arr_p = malloc(ydim * sizeof(int *));
    if (!arr_p)
        return -1; // memory allocation failed

    for (int j = 0; j < ydim; j++) {
        arr_p[j] = malloc(xdim * sizeof(int));
        if (!arr_p[j]) {
            // memory allocation failed, release memory
            // will have to go through previously allocated rows
            for (int i = 0; i < j; i++) {
                free(arr_p[i]);
            }
            free(arr_p);
            return -1;
        }
        for (int i = 0; i < xdim; i++) {
            // fill matrix with values, multiplication table
            arr_p[j][i] = (i+1) * (j+1);
        }
    }

    printArray(arr_p, xdim, ydim);

    // release the memory
    for (int j = 0; j < ydim; j++) {
        free(arr_p[j]);
    }
    free(arr_p);
}

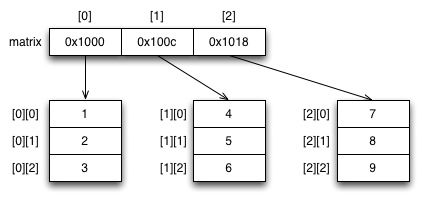
This example continues modifying the previous simple matrix example. The printArray() function is same as before, but it is now called with two-dimensional array that is allocated from heap. Now the data type of arr_p variable is int **, a pointer to pointer(s), because with arrays a pointer points to the beginning of array.

The first degree array can be indexed using arr_p[j] (which is the same as *(arr_p + j), as always). Because there is one defererence, one "star" of the data type goes away. Therefore the data type of arr_p[j] is int *, i.e., a one-dimensional array. This is why on line 22 the number of rows is multiplied by sizeof(int *) in a malloc call: int * is the type of single member in the first-degree array.

Each of the arr_p[j] arrays can be indexed again with arr_p[j][i] (which is equivalent with *(*(arr + j) + i)). There is another dereference, and one "star" of the data type goes away. Therefore arr_p[j][i] is of type int.

Variables ydim and xdim hold the array dimensions. In this variant, the first-degree dimension is represented by ydim, as for vertical lines, and second-degree is for horizontal dimensions, but this could be also the other way around.

The same principle can be generalized into any number of dimensions: there could be three-dimensional arrays or four-dimensional arrays. The data types would just have more "stars" involved.

Arrays of strings

A common case of array of pointers is an array of strings. Essentially this is a two-dimensional array as well, because strings are arrays of characters. In this case the different columns of arrays can have different lengths. The following code represents the names of the months as an array:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

#include <stdio.h>

int main(void) {
    char *months[] = { "January", "February", "March", "April", "May",
               "June", "July", "August", "September", "October",
               "November", "December" };

    for (int i = 0; i < 12; i++) {
        printf("%s\n", months[i]);
    }
}

In the above case the strings in the array are constant strings: they cannot be modified. Otherwise they are used as normal array members. A single character of the months array could be accessed using months[j][i], where i indicates the character in month string j. Because printf() format specifier '%s' on above line 9 assumes char * type, only the first-degree index is needed.

The strings can also be defined as changeable strings in a similar way as in the basic case. Then the definition of months array, could be, for example:

1
2
3

char months[12][20] = { "January", "February", "March", "April", "May",
           "June", "July", "August", "September", "October",
           "November", "December" };

The above definition declares months as an array of 12 strings, and for each string 20 bytes are reserved. We could omit 12 in the definition, and just use char months[][20], because the compiler will see the needed array length from the initialization list, but the size of each string must be given, so that the compiler can build the array appropriately. The strings will be located on consecutive memory locations, 20 bytes each.

Command line parameters are a traditional form of passing instructions and information to the program when it is started from a command line terminal interface (or from a script). With graphical user interfaces and embedded mobile gadgets the command line parameters may not have much significance, but because they are a very common interface for controlling the application behavior in Unix systems, and timely to the theme of this module, we will discuss them briefly.

Until this point we have seen several examples of a main function that does not have parameters. The main function also has an alternative form that allows passing the command line arguments that were given when program was started. The command line parameters are represented as an array of strings. The following small piece of code illustrates how they work:

1
2
3
4
5
6
7
8
9

#include <stdio.h>

int main(int argc, char *argv[]) {
    printf("This program was called with %d parameters\n", argc);
    printf("They were (including the program name itself):\n");
    for (int i = 0; i < argc; i++) {
        printf("%s\n", argv[i]);
    }
}

Here the main function comes with two parameters: argc tells the number of command line parameters, and argv is an array of strings, where each element contains one command line parameter. The program name itself is the first command line parameter, so there at least one array member is always included. For example, when user types the following on the command line:

./program one two three

argc will be 4, and the argv array will have the following content: { "./program", "one", "two", "three" }.

A common format on command line is to use command line options that start with dash (-) and are followed by a single character. Such options can be standalone, or come with an additional parameter. For example, the tail command below:

tail -f -q -n 10 file.txt

has three options, 'f', 'q' and 'n'. 'f' and 'q' are without additional parameters, by 'n' comes with an integer parameter 10. Finally, there is a command line parameter that does not follow the option format. Typically the options can be given in any order.

Binary system

In binary (base-2) numeral system all numbers are presented with two symbols (bits), 0 or 1. Binary arithmetics have been traditionally significant in computer systems based on digital electronic circuitry, and therefore binary operations come across in low-level implementations. In computer, all numbers or datatypes are built from combinations of bits. Binary operations are also useful in packing information efficiently in small space, and for example, various low-level communication protocols rely on binary operations to efficiently transmit information over a communication link.

Standard C does not support representing numbers in binary format (although there are extensions to support it in many compilers). Therefore, hexadecimal (base-16, i.e., base-2⁴) numbers are a often used together with binary numbers, because each hexadecimal digit can be represented with four bits, making them fairly handy format for binary operations. Hexadecimal system has 16 symbols: in addition to numbers 0 - 9, letters A to F are used to indicate decimal values 10 - 15. The table below illustrates the close connection between binary representation and hexadecimal representation.

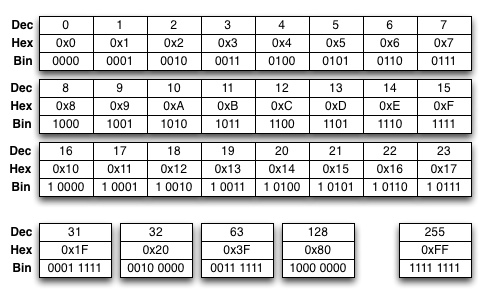
Following the logic shown in the table one can also do conversions between longer hexadecimal numbers and their binary representation. For example, a 16-bit (unsigned short) hexadecimal number 0xD2A0 is 1101 0010 1010 0000 in binary format.

Bitwise operators

The bit patterns can be manipulated through bitwise operators. The following four bitwise operators are available:

• bitwise AND (&): A & B is 1 if both bit A and bit B are 1. If either of them is 0, A & B is 0 as well.

• bitwise OR (|): A | B is 1 if either bit A or bit B is 1. If both of them are 0, A | B is 0.

• bitwise exclusive OR (^): A ^ B is 1 if the state of bit A is different from state of bit B. If both A and B are 1 or 0, then A ^ B is 0.

• one's complement NOT: ~A converts bit 1 to 0, and vice versa.

It is important to distinguish between the logical operators (e.g., &&, || and !) and bitwise operators. The logical operators result in integer values 0 or 1, while bitwise operators do manipulations on bit level, meaning that the resulting value can be some other integer as well, depending how the individual bits were affected by the bitwise operation -- remembering that all numbers are built from combinations of bits.

The below table shows an example of these operations in two unsigned char - type values, 0x69 and 0xCA.

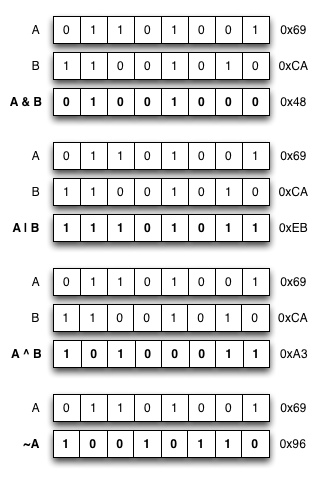
The above examples can be written in C code as follows.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

#include <stdio.h>

int main(void) {
    unsigned char a = 0x69;  // 01101001
    unsigned char b = 0xca;  // 11001010

    printf("a & b = %02x\n", a & b);

    unsigned char c = a | b;

    printf("a | b = %02x\n", c);

    b ^= a;  // b = b ^ a
    printf("a ^ b = %02x\n", b);

    printf("~a = %02x\n", ~a);
    printf("~a & 0xff = %02x\n", ~a & 0xff);
}

This will print out:

a & b = 48
a | b = eb
a ^ b = a3
~a = ffffff96
~a & 0xff = 96

The outcome of ~a may be surprising, and relates to integral promotion: C internally converts small integer data types (such as char or short) into the underlying architecture's "native" integer type before arithmetic operations, for optimized performance. In many cases this is not visible to the programmer because the high-end bits tend to remain zero, but here the bitwise negation turns the bits to 1, which reveals the actual data length on printout. However, we can use bitwise AND to reset the higher-order bits, as done on line 17.

In addition to the logical operators, bitwise shift operators can be applied to an expression. The << operator shifts the bits left a given number of steps. For example A << 1 shifts the bits left by one step, and A << 4 shifts the bits left by four steps. Similarly, A >> 1 shifts the bits right by one step, and A >> 4 shifts the bits right by fours steps. When bits are shifted right by N positions, the rightmost N bits are lost, and the leftmost N bits will be set to 0. Correspondingly, when bits are shifted left by N positions, the N leftmost bits are lost, and N rightmost bits become 0. Below table illustrates a few bit shift operations.

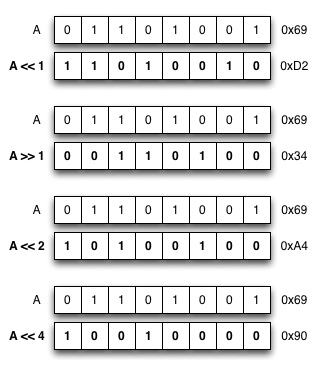
The following program implements function printBits that uses the bit shift operations, together with logical AND to output a binary presentation of the given unsigned char value, and tests its use with a couple of values shown above.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

#include <stdio.h>

void printBits(unsigned char value)
{
    for (int i = 7; i >= 0; i--) {
        // (1 << i) generates value where only i'th bit is set
    // value & (1 << i)) is non-zero only if i'th bit is set in value
        if (value & (1 << i))
        printf("1");
    else
        printf("0");
    }
}

int main(void) {
    unsigned char a = 0x69;
    printf("0x69 = ");
    printBits(a);
    printf("\n0x69 << 2 = ");
    printBits(a << 2);
    printf("\n");
}

The program outputs:

0x69 = 01101001
0x69 << 2 = 10100100

Bit masks are used to operate on selected bit or set of bits. State of bits can be investigated using the bitwise AND operator, and bit masks can be combined using the bitwise OR operator. The result of bitwise AND operation is true (non-zero) only if at least one of the indicated bits is set. The below example investigates state of a few bits, and converts the highest four bits in variable a into integer.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

#include <stdio.h>

int main(void) {
    unsigned char a = 0x36;  // 00110110
    if (a & 0x2) {
        // Second bit is set, true in this case
    }
    if (a & 0x1) {
        // First bit is set, not true in this case
    }
    if (a & 0xf0) {  // are any of the highest four bits set?
        // convert the highest four bits to integer
        int b = (a & 0xf0) >> 4; // b == 3
    }
}

Programs can use flags to represent some state in a system. A flag can either be on or off, i.e., it can be naturally represented with a single bit. Such presentation is also very efficient where space matters: a single char - type variable can store 8 different flags, because it consists of 8 bits. Bitwise operations can be used to evaluate and set the state of individual flags.

The following example operates an imaginary file, that can have four types of permissions separately for the file owner and a "group". The permissions are presented by flags that can either be on or off, in different combinations. A single unsigned char is sufficient for representing read, write, execute and delete permissions, separately for an owner and a group.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

#include <stdio.h>

typedef unsigned char MyFlags;

// Owner permissions
const MyFlags CanRead = 0x1;
const MyFlags CanWrite = 0x2;
const MyFlags CanExecute = 0x4;
const MyFlags CanDelete = 0x8;

// Group permissions
const MyFlags GroupCanRead = CanRead &lt;&lt; 4;       // 0x10
const MyFlags GroupCanWrite = CanWrite &lt;&lt; 4;     // 0x20
const MyFlags GroupCanExecute = CanExecute &lt;&lt; 4; // 0x40
const MyFlags GroupCanDelete = CanDelete &lt;&lt; 4;   // 0x80

typedef struct {
    const char *name;
    MyFlags perms;
} File;

int main(void) {
    File fileA;
    fileA.name = "File 1";
    fileA.perms = CanRead | CanWrite; // can read and write, but not execute
    printf("flags 1: %02x\n", fileA.perms);

    if (fileA.perms & CanRead) {
        printf("reading is possible\n");
    }
    if (fileA.perms & GroupCanRead) {
        // Group cannot read, so we can't get here
        printf("group reading is possible\n");
    }
    fileA.perms |= GroupCanRead; // now also group can read
    printf("flags 2: %02x\n", fileA.perms);

    // zeroing CanWrite and GroupCanWrite
    fileA.perms &= ~(CanWrite | GroupCanWrite);

    // print the final state of flags
    printf("flags 3: %02x\n", fileA.perms);
}

The above program will output the following:

flags 1: 03
reading is possible
flags 2: 13
flags 3: 11

Byte order

The binary numbers larger than one byte (e.g., short integers or integers) can be encoded in different ways in different architectures. The programmer needs to take this into account if exporting data outside the local machine (for example, when storing to portable storage or writing data to network). The order of bytes may either be big-endian (the most significant byte is in smallest memory address, and the least significant byte is largest memory address), of it could be little-endian (the least significant byte is in smallest memory address). For example, the Intel-based architectures (i.e., most current computers) are commonly little-endian, but many standards (e.g. for network protocols) require big-endian byte order. There are functions for byte order conversions (ntohs, ntohl, htons, htonl), but the conversion is can be made also by byte-by-byte assignments, and applying bit shift operations appropriately (see example below). Below is an example of 32-bit integer, and its representation in the two formats, when looking the same memory space on byte-by-byte level, and a piece of code that does conversion to big-endian byte order.

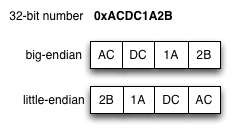
1
2
3
4
5
6

unsigned int num = 0xACDC1A2B;
unsigned char big_endian[4];
big_endian[0] = num >> 24;  // AC
big_endian[1] = (num >> 16) & 0xff;  // DC
big_endian[2] = (num >> 8) & 0xff; // 1A
big_endian[3] = num & 0xff; // 2B